A equação mais perigosa do mundo e o efeito do tamanho da amostra nos resultados

estatistica

Introdução

Nesta thread no subreddit de Data Science, um usuário fez o seguinte comentário:

So basically, I was asked to make inference on 10 people and expect those to generalize to the entire study population. I said the study was poorly designed, and that if I made up random numbers we would do a better job of understanding the customer base.

É muito comum pessoas que não são muito familiares com conceitos de inferência estatística ignorar o fato de que tomar conclusões a partir de amostras muito pequenas pode ser bastante perigoso.

Neste artigo escrito por Howard Wainer (Aviso: Link para PDF), são citados dois motivos para que uma equação possa ser perigosa: o fato de elas serem conhecidas e o fato de elas serem desconhecidas. A equação de Moivre, que descreve o desvio padrão da distribuição amostral da média, se encontra no segundo caso:

\(\sigma_{\bar{x}}= \frac{\sigma}{\sqrt{n}}\)

Onde \(\sigma_{\bar{x}}\) é o erro padrão da média, \(\sigma\) o desvio padrão da amostra e \(n\) o tamanho da amostra. Em outras palavras, dado que \(\sigma\) é um parâmetro conhecido, quanto menor o tamanho da amost, maior será erro da estimativa, que corresponde a variação da média amostral em relação à média da população. O paper inteiro é muito bom e fácil de ler, então recomendo a leitura.

O objetivo deste post é um exercício simples para mostrar o efeito do tamanho da amostra na variabilidade dos resultados, mesmo quando se sabem os valores verdadeiros dos parâmetros de toda a população.

Geração dos dados por simulação

library(tidyverse)

O primeiro passo é gerar uma população de dados cujos parâmetros são conhecidos. Aqui, duas variáveis aleatórias ´x´ e ´y´ são definidas, em que x é uma variável aleatória e ´y´ deriva de x, com algum ruído:

n <- 1e5
set.seed(123)
x <- rnorm(n, mean = 0, sd = 0.5)
y <- 2 * x + 5 + rnorm(n, mean = 0, sd = 0.25)

df <- data.frame(x = x, y = y)
mod_populacao <- lm(y ~ x, data = df)
summary(mod_populacao)
## 
## Call:
## lm(formula = y ~ x, data = df)
## 
## Residuals:
##     Min      1Q  Median      3Q     Max 
## -1.0972 -0.1685 -0.0002  0.1683  1.0506 
## 
## Coefficients:
##              Estimate Std. Error t value Pr(>|t|)    
## (Intercept) 5.0013045  0.0007937    6302   <2e-16 ***
## x           1.9986648  0.0015877    1259   <2e-16 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## Residual standard error: 0.251 on 99998 degrees of freedom
## Multiple R-squared:  0.9406, Adjusted R-squared:  0.9406 
## F-statistic: 1.585e+06 on 1 and 99998 DF,  p-value: < 2.2e-16

Como esperado, a partir do modelo de regressão obtido acima a partir da população de parâmetros são conhecidos que o processo de geração da variável resposta ´y´ pode ser representado pela equação abaixo:

\(y = 2x + 5 + \epsilon\)

O histograma dos resíduos do modelo é mais uma evidência de que o modelo obtido possui boas propriedades:

hist(resid(mod_populacao),
     main = "Distribuição dos resíduos do modelo da população",
     xlab = NULL)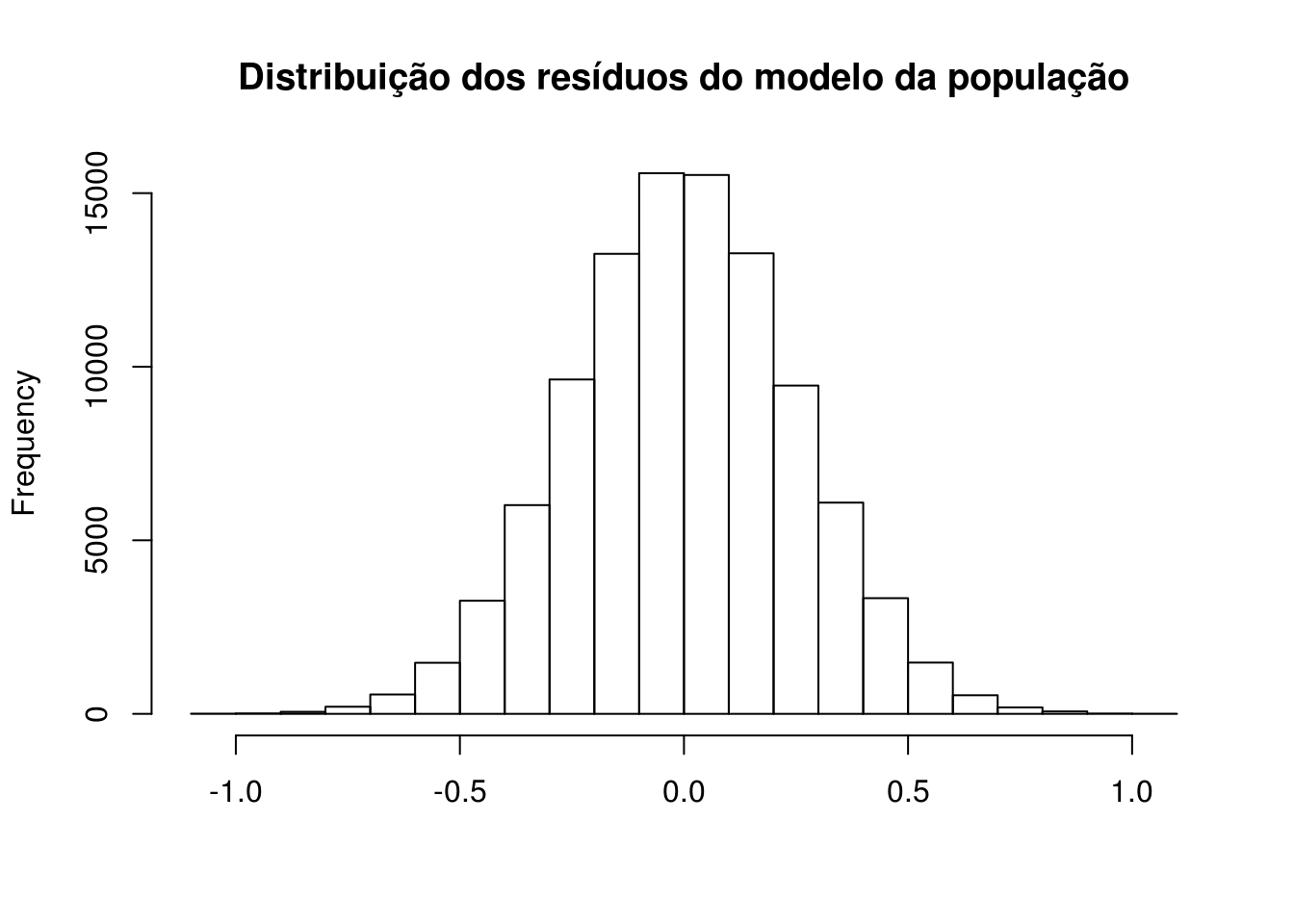

Assim, se tirarmos uma amostra da população e criarmos um modelo \(y = f(x)\), os parâmetros do modelo dessa amostra serão os mesmos ou próximos ao da população, correto? Depende de seu tamanho.

Geração das amostras

A função abaixo cria 1000 amostras de tamanho sample_size do dataframe df dos dados da população e, para cada uma das amostras, ajusta um modelo de regressão linear, extrai o coeficiente de x da regressão e retorna um dataframe com os resultados:

coef_x_sample <- function(sample_size){
  repl <- purrr::rerun(1000, sample_n(df, sample_size))
  
  vec_coef_x <- repl %>% 
    map(~ lm(y ~ x, data = .)) %>% 
    map_dbl(~ coef(.)["x"])
  
  data.frame(size = sample_size, coef_x = vec_coef_x)
}

# exemplo
set.seed(123)
head(coef_x_sample(10))
##   size   coef_x
## 1   10 2.065196
## 2   10 2.320681
## 3   10 2.142100
## 4   10 2.069578
## 5   10 2.036510
## 6   10 1.704862

Nas 6 primeiras amostras de tamanho 10, o coeficiente de x foi desde 1,70 a 2,32, mostrando uma certa variabilidade.

O código abaixo repete o processo acima para valores diferentes do tamanho da amostra:

vec_samp_size <- c(5, 10, 15, 20, 50, 75, 100, 150, 200, 250, 500, 750, 1000, 5000)

df_result <- vec_samp_size  %>% map_dfr(coef_x_sample)

df_result <- df_result %>% 
  mutate(size = factor(size, levels = vec_samp_size))

Análise dos resultados

Vários gráficos podem ser feitos para ilustrar os resultados da variabilidade do parâmetro da regressão em funcão do tamanho da amostra, como o boxplot abaixo:

df_result %>% 
  ggplot(aes(x = size, y = coef_x)) + 
  geom_boxplot() + 
  scale_y_continuous(breaks = seq(-4, 4, by = 1)) + 
  labs(x = NULL, y = NULL,
       title = "Variabilidade do coeficiente de x em função do tamanho da amostra") + 
  theme_minimal()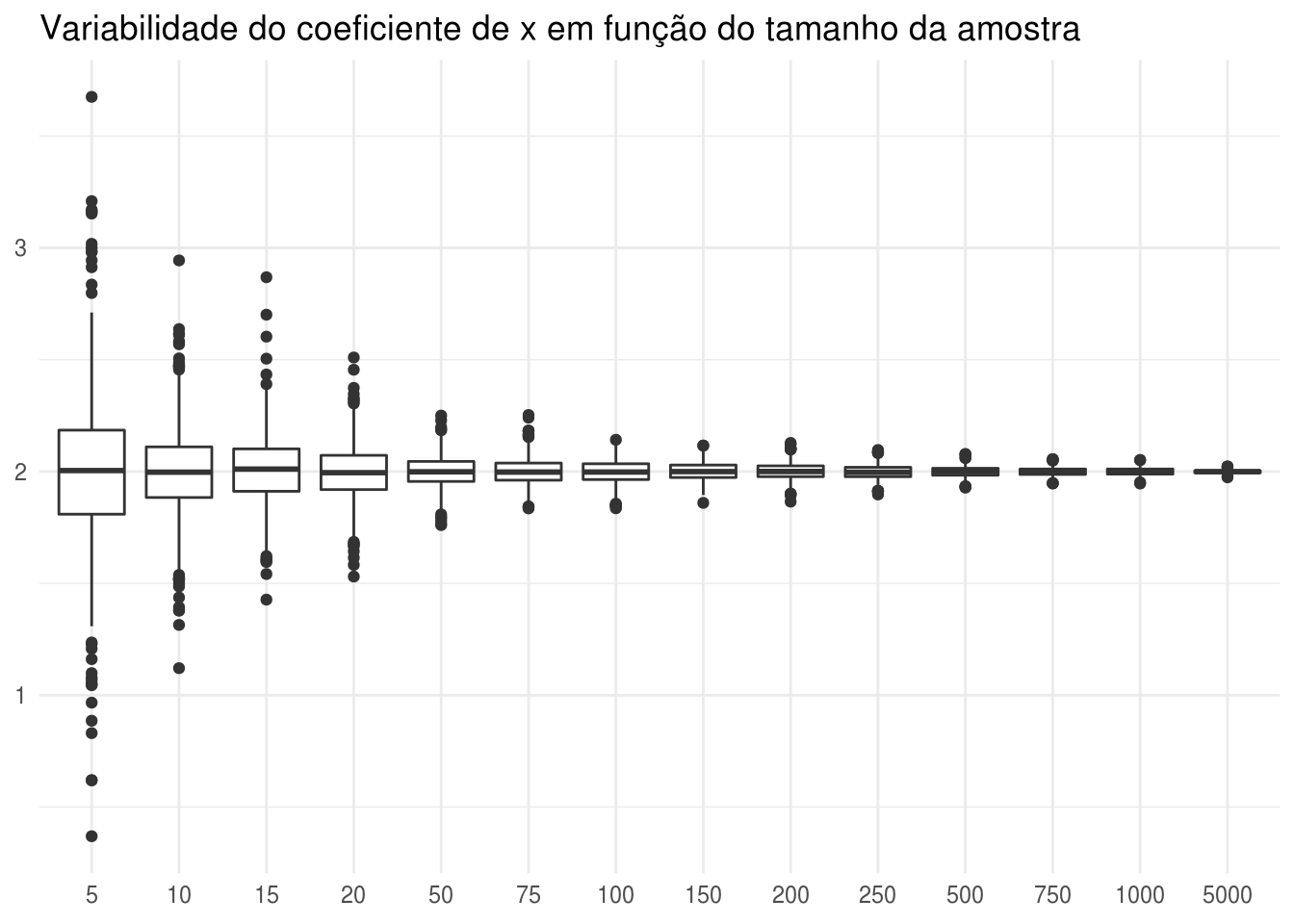

O gráfico acima mostra que, apesar de a mediana ser aproximadamente 2 em todos os tamanhos amostrais testados, a variabilidade é muito maior nas menores amostras. A medida que se aumenta o número de indivíduos na amostra, a distribuição dos resultados converge para o valor verdadeiro. Para amostras de 5 indivíduos, foram observados resultados no seguinte intervalo:

# intervalo para menor tamanho amostral
range(df_result$coef_x[df_result$size == "5"])
## [1] 0.3693973 3.6749739
# intervalo para maior tamanho amostral
range(df_result$coef_x[df_result$size == "5000"])
## [1] 1.973962 2.022880

Ou seja, mesmo que uma amostra seja oriunda de uma população descrita por parâmetros já determinados, usar resultados de uma amostra pequena pode levar a conclusões erradas.

 
comments powered by Disqus