Calculadora do Cidadão
Devido a um fenômeno econômico chamado de Inflação, o valor do dinheiro muda com o tempo. R\$100,00 hoje não possuem o mesmo valor monetário ou poder de compra que R\$100,00 daqui a 10 anos, ou mesmo 10 anos atrás. Uma técnica que pode ser usada para corrigir esse efeito é a de deflacionar esses valores, como mostrado neste post do blog Análise Macro. Um outro serviço que pode ser usado é a Calculadora do Cidadão, um produto desenvolvido pelo Banco Central do Brasil para facilitar o trabalho das pessoas que desejam corrigir valores pela inflação de maneira muito simples: Basta adicionar os dados nesta página de data inicial, data final e valor a ser corrigido. A ferramenta então informará o índice de correção no período, o valor percentual correspondente e o valor corrigido na data final. Assim, descobrimos que, por exemplo, R\$1,00 em Janeiro de 2008 equivale a R\$1,81 em Janeiro de 2018, de acordo com o IPCA-E, índice desenvolvido pelo IBGE.
Além da correção de valores pela inflação, a Calculadora do Cidadão fornece outros serviços de atualização de valores monetários, como:
- TR: Taxa Referencial. Taxa obtida a partir das médias dos CDBs de 30 dias a taxas pré-fixadas praticadas por bancos comerciais.
- Poupança: Os rendimentos da poupança são creditados mensalmente, na data equivalente à data de aplicação (data-base). Dessa forma, se uma aplicação na poupança for resgatada antes de chegar à sua primeira data-base, não fará jus a qualquer correção, e o valor final será igual ao inicial.
- Selic: Utiliza para correção a taxa apurada no Selic. Esta taxa é obtida mediante o cálculo da taxa média ponderada e ajustada das operações de financiamento por um dia, lastreadas em títulos públicos federais e cursadas no referido sistema ou em câmaras de compensação e liquidação de ativos, na forma de operações compromissadas.
- CDI: Depósito Interfinanceiro. É uma operação realizada exclusivamente entre instituições financeiras, para permitir a troca de reservas bancárias entre elas. Tem registro no CETIP - Câmara de Custódia e Liquidação. Foi autorizada pelo Decreto-Lei nº 2.284/86 e regulamentada pela Resolução nº 1.647/89. A taxa do CDI é calculada como a média das taxas das operações registradas, ponderadas pelos volumes negociados, em determinado dia útil.
Uma das utilizações dessas ferramentas é poder saber, por exemplo, quanto uma aplicação de R\$1000,00 teria rendido nessas diferentes modalidades de renda fixa em um determinado período no passado.
Pensando em todas essas utilidades da Calculadora do Cidadão, eu criei há um tempo o pacote calcCidadao, cujo objetivo é automatizar as consultas de tais informações na plataforma do BCB. Um ponto negativo do pacote é que, como o Banco Central não fornece uma API para a Calculadora do Cidadão, as funções do calcCidadao funcionam por meio de Web Scraping, o que pode tornar o código lento para muitas requisições (não é a toa que eu paralelizei as iterações neste post). Neste post, darei uma sugestão de como o pacote pode ser usado na análise de investimentos.
Funções básicas do pacote
library(tidyverse)
library(calcCidadao)
library(lubridate)
library(quantmod)
library(furrr)O pacote possui uma função para cada tipo de correção fornecida pela Calculadora do Cidadão:
ls("package:calcCidadao")## [1] "inflation_indices" "return_cdi" "return_inflation"
## [4] "return_poupanca" "return_selic" "return_tr"inflation_indices é uma função que retorna os nomes e códigos dos índices de inflação que podem ser usados como input na função return_inflation:
print(inflation_indices())## IGP-M IGP-DI INPC IPC-A
## "00189IGP-M" "00190IGP-DI" "00188INPC" "00433IPC-A"
## IPCA-E IPC-BRASIL IPC-SP
## "10764IPC-E" "00191IPC-BRASIL" "00193IPC-SP"Para corrigir um valor de 10 anos atrás de acordo com o IPCA-E, fazemos assim:
d1 <- as.Date("2008-01-01")
d2 <- as.Date("2018-01-01")
return_inflation("IPCA-E", start_date = d1, end_date = d2)## [1] 1.811145O fator de correção do IPCA-E no período é de 1,811145. Assim, R\$1000 em 01/01/2008 valiam o equivalente a R\$1811,45 10 anos depois.
O mesmo pode ser feito com os índices de renda fixa. Quanto o CDI e a Selic renderam a mais que a Poupança nesse mesmo período?
renda_fixa_10_anos <- c(
return_cdi(d1, d2),
return_selic(d1, d2),
return_poupanca(d1, d2)
)
renda_fixa_10_anos## [1] 2.785752 2.801270 2.009103Os resultados acima mostram algo que já é sabido: A poupança é um investimento muito pior que investimentos atrelados a CDI e Selic (a não ser que a taxa seja muito ruim).
Estudo de caso para o pacote: Análise de um Título Pré-Fixado
Em um fórum de investimentos que participo, havia uma discussão sobre como avaliar a “qualidade” de um título CDB pré-fixado de um prazo relativamente longo, como 6 anos. Mesmo que a taxa seja atrativa (um rendimento de 14% ao ano pode fazer o capital investido dobrar no período), 6 anos é um prazo muito longo em um país onde até o passado é imprevisível. É natural surgir perguntas como E se a inflação acumulada no período for maior? ou E se um título pós-fixado a 100% do CDI render mais, me fazendo ter um custo de oportunidade?.
De fato, a não ser que você trabalhe na Empiricus, não dá para saber como estará a Selic e a inflação ao longo dos próximos 6 anos. É simplesmente impossível prever variáveis tão complexas em um período tão distante no período no futuro. Contudo, é possível ter alguma noção desses valores a partir de simulação de rendimentos passados do mesmo intervalo de tempo.
Vamos então tomar como exemplo um produto que eu recebi por e-mail da Easynvest: um CDB prefixado de 15,07% ao ano do Banco Pine com prazo de 6 anos. Para calcular seu retorno líquido ao final do período, basta usar uma fórmula de juros compostos:
juros_compostos <- function(i, t, imposto){
bruto <- (1 + i)^t - 1
liquido <- bruto * (1 - imposto)
liquido
}
# taxa de 15.07%aa para 6 anos, considerando 15% de IR
retorno_cdb <- juros_compostos(0.1507, 6, 0.15)
retorno_cdb## [1] 1.123293# montante liquido no resgate para um capital de 1000 reais
valor_liquido_cdb <- round(1000 * (1 + retorno_cdb), 2)Como vimos, o CDB mais que dobra o dinheiro investido no período. Mas será que isso é suficiente para bater a inflação e o CDI? Isso pode ser respondido por meio de simulação.
O método da simulação consiste em obter o retorno desses indicadores para cerca de 200 pares de datas com 6 anos de diferença entre elas.
# data para gerar vetor de datas para tras
data_base <- floor_date(today() - 31, "month")
qtd_sim <- 200
# gerar vetor de datas começando no primeiro dia de cada mes
d1 <- d2 <- sort(unique(floor_date(data_base - ddays(seq_len(qtd_sim) * 30), "month")))
# descontar para a data inicial 6 anos
year(d1) <- year(d1) - 6
# exemplo de como ficou
head(tibble(d1, d2))## # A tibble: 6 x 2
## d1 d2
## <date> <date>
## 1 1995-11-01 2001-11-01
## 2 1995-12-01 2001-12-01
## 3 1996-01-01 2002-01-01
## 4 1996-02-01 2002-02-01
## 5 1996-03-01 2002-03-01
## 6 1996-04-01 2002-04-01Temos então dois vetores de datas d1 e d2 em que \(d{_2}_t \simeq (365 * 5) + d{_1}_t\). Esses serão usados como inputs das funções do calcCidadao.
Como são muitas requisições, o processo pode ser bem lento. Por isso, eu uso o pacote furrr para paralelizar as iterações:
plan(multiprocess)
inflacao_6 <- furrr::future_map2_dbl(
d1, d2, ~return_inflation("IPCA-E", start_date = .x, end_date = .y),
.progress = FALSE)
cdi_6 = furrr::future_map2_dbl(
d1, d2, ~return_cdi(start_date = .x, end_date = .y),
.progress = FALSE)
# salvar resultados em um tibble
df_results <- tibble(
data_aplicacao = d1,
data_resgate = d2,
# no caso dos valores extraidos pelas funcoes do calcCidadao,
# nao eh necessario somar 1, visto que as funcoes ja retornam
# o indice de correcao
valor_corrigido_ipca = round(1000 * inflacao_6, 2),
valor_corrigido_cdi = round(1000 * cdi_6, 2)
)head(df_results)## # A tibble: 6 x 4
## data_aplicacao data_resgate valor_corrigido_ipca valor_corrigido_cdi
## <date> <date> <dbl> <dbl>
## 1 1995-11-01 2001-11-01 1498. 3603.
## 2 1995-12-01 2001-12-01 1484. 3552.
## 3 1996-01-01 2002-01-01 1473. 3506.
## 4 1996-02-01 2002-02-01 1456. 3471.
## 5 1996-03-01 2002-03-01 1445. 3435.
## 6 1996-04-01 2002-04-01 1447. 3407.Já que estamos falando de comparação de investimentos, por que não incluir também a renda variável no estudo? O código abaixo extrai preços de fechamento ajustados do IBOVESPA, agrega os dados pelo primeiro dia de operação de cada mês, e calcula o “valor corrigido” usando o preço de fechamento ajustado após 72 meses.
ibov <- quantmod::getSymbols("^BVSP", from = min(d1), auto.assign = FALSE)
head(Ad(ibov))## BVSP.Adjusted
## 1995-11-01 4099.8
## 1995-11-02 NA
## 1995-11-03 4158.8
## 1995-11-06 4094.3
## 1995-11-07 4111.2
## 1995-11-08 4117.1df_ibov <- tibble(date = index(ibov), price = as.numeric(Ad(ibov))) %>%
na.omit() %>%
group_by(mes = floor_date(date, "month")) %>%
filter(date == min(date)) %>%
ungroup() %>%
mutate(fator_ibov = dplyr::lead(price, 72)/price,
valor_corrigido_ibov = round(1000 * fator_ibov, 2)) %>%
select(data_aplicacao = mes, valor_corrigido_ibov)# juntar em um dataframe so
df_completo <- left_join(df_results, df_ibov, by = "data_aplicacao")
names(df_completo)[3:5] <- str_remove_all(names(df_completo)[3:5], "valor_corrigido_")
df_completo[1,]## # A tibble: 1 x 5
## data_aplicacao data_resgate ipca cdi ibov
## <date> <date> <dbl> <dbl> <dbl>
## 1 1995-11-01 2001-11-01 1498. 3603. 2778.No exemplo acima, apenas a inflação não foi superior ao nosso CDB prefixado de exemplo: Tanto o CDI como o IBOV eram opções melhores (partindo do pressuposto que em 01/11/1995 você era capaz de prever tais índices 6 anos depois).
O gráfico abaixo ilustra a distribuição dos resultados de cada índice comparado com o CDB de interesse:
df_completo %>%
gather(indice, novo_valor, ipca:ibov) %>%
ggplot(aes(x = novo_valor)) +
geom_histogram(binwidth = 100) +
geom_vline(xintercept = valor_liquido_cdb, color = "red", linetype = "dashed") +
facet_wrap(~ indice, scales = "fixed", ncol = 1) +
theme_minimal() +
labs(x = "Valor corrigido líquido (R$)", y = NULL,
title = "CDI, IBOV e Inflação vs. CDB Prefixado de 15,07% a.a.",
subtitle = "Prazo de 6 anos")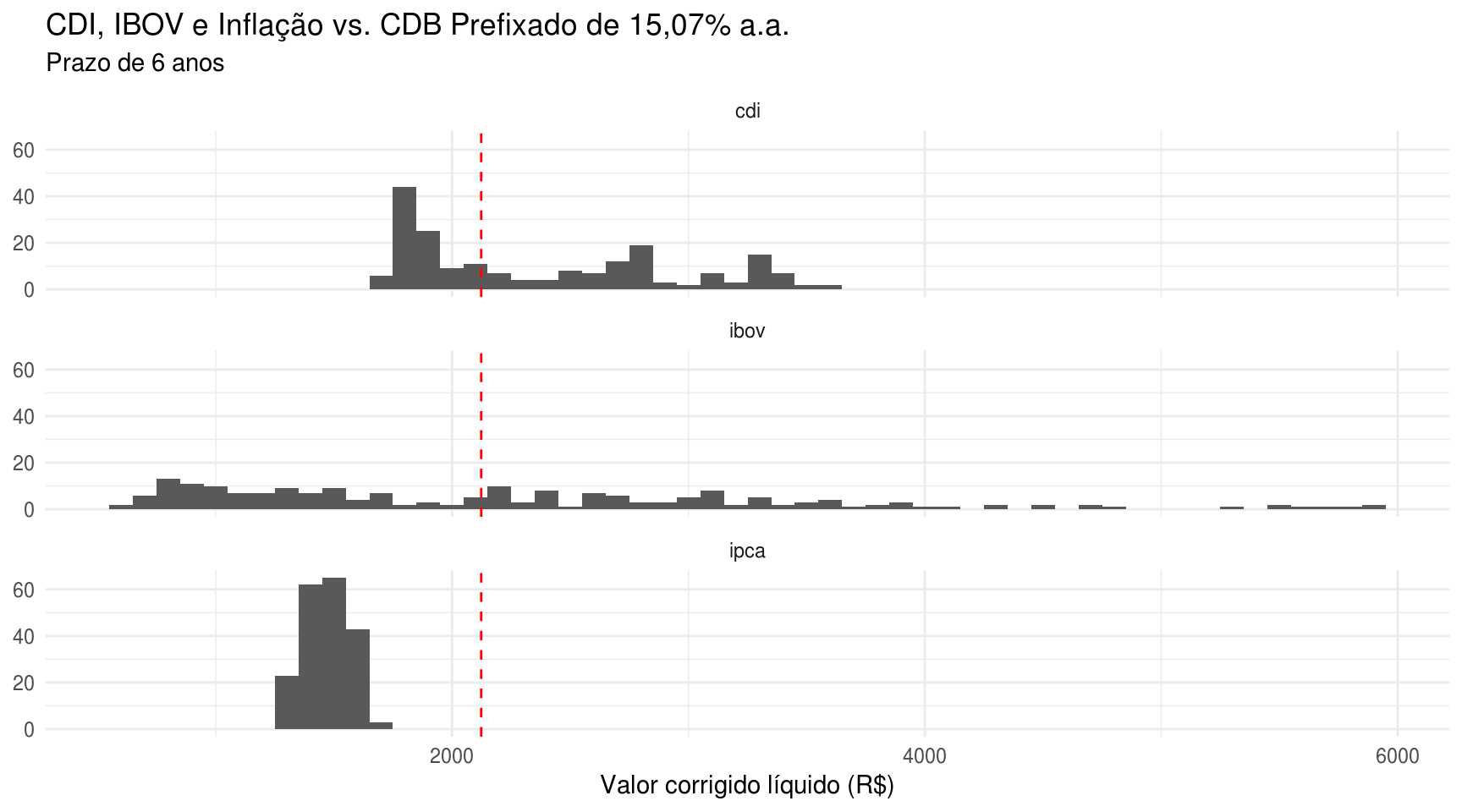
O gráfico acima mostra que esse CDB prefixado pode não ser um investimento tão bom assim. Muitas vezes o CDI e o IBOV trouxeram resultados melhores para o mesmo intervalo de 6 anos. Numericamente, os resultados são:
df_completo %>%
summarise_at(vars(ipca:ibov), ~ mean(.x >= valor_liquido_cdb, na.rm = TRUE))## # A tibble: 1 x 3
## ipca cdi ibov
## <dbl> <dbl> <dbl>
## 1 0. 0.533 0.487Ou seja: o CDI e o IBOV foram melhores que o CDB em 53,3% e 48,7% das vezes, respectivamente. Levando em conta que o Ibovespa se trata de renda variável e apresenta um risco maior (levando em conta que o CDB possui proteção do FGC), pode-se dizer que o resultado do CDB é aceitável em comparação com a bolsa de valores.
Será que a distribuição desses resultados é uniforme com o tempo? Certamente não, visto que tanto o Ibovespa quanto a taxa Selic (que apresenta resultados muito parecidos com o CDI) variaram muito desde 1995. Por isso a utilidade do gráfico abaixo:
df_completo %>%
gather(indice, novo_valor, ipca:ibov) %>%
ggplot(aes(x = data_aplicacao, y = novo_valor)) +
geom_line(aes(color = indice)) +
geom_hline(yintercept = valor_liquido_cdb, linetype = "dashed") +
geom_hline(yintercept = 1000, linetype = "dotted") +
theme_minimal() +
scale_x_date(date_breaks = "1 year", date_labels = "%Y") +
scale_y_continuous(breaks = scales::pretty_breaks(n = 6)) +
annotate("rect", fill = "red", alpha = 0.15,
xmin = as.Date(-Inf), xmax = as.Date(Inf),
ymin = -Inf, ymax = 1000) +
labs(x = NULL, y = "R$",
title = "Valor de R$ 1000 corrigido por diferentes índices",
subtitle = "Resultados em função da data de aplicação apos um período de 6 anos") +
theme(panel.grid.minor.x = element_blank())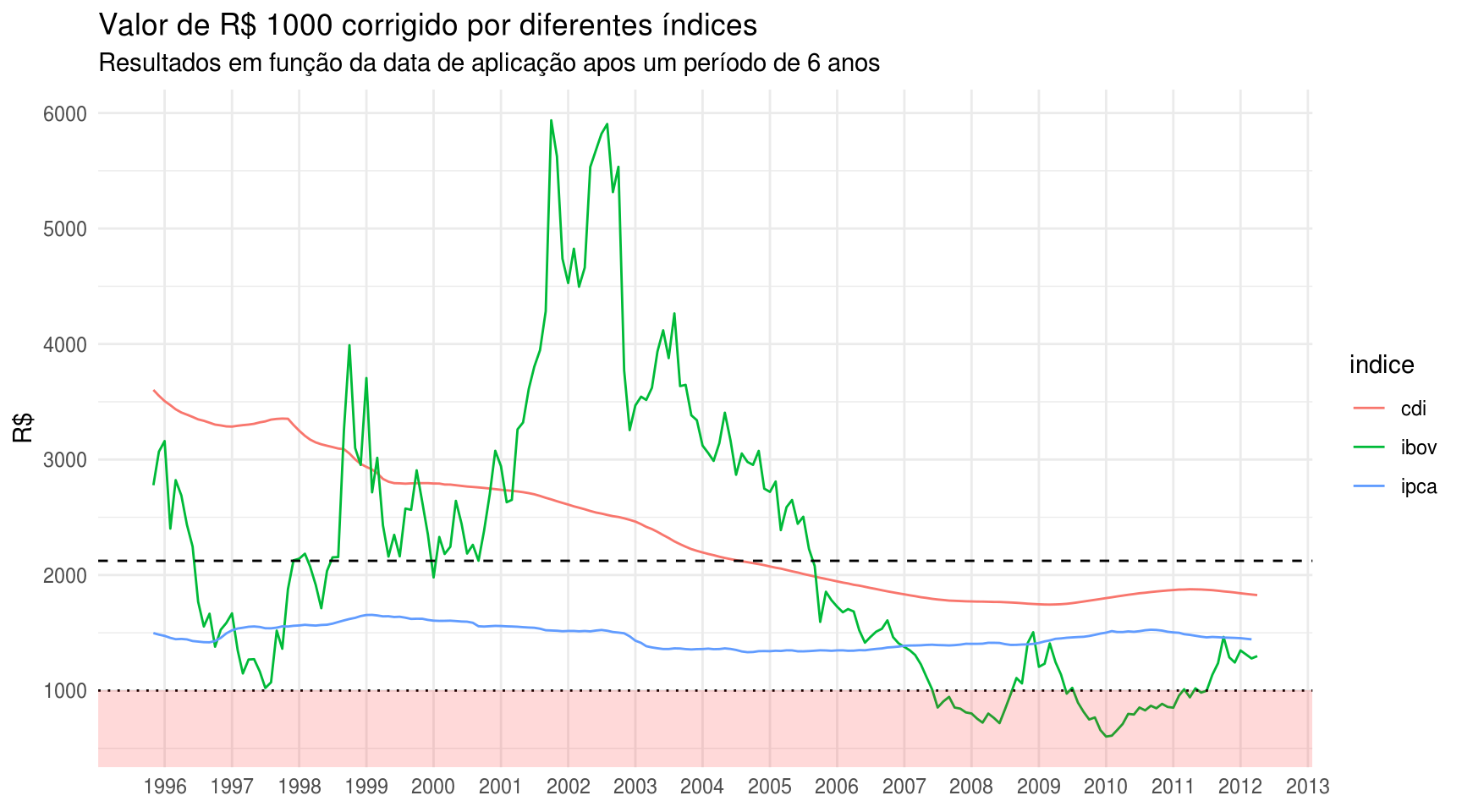
O que o gráfico acima mostra é que observar os resultados levando em conta o fator tempo muda completamente a interpretação: a partir do fim de 2005, nenhum investimento tem proporcionado um rendimento líquido superior ao CDB préfixado de 15,07% ao ano. Outra observação interessante a partir do gráfico é comprovar que a bolsa de valores é muito mais volátil que a renda fixa, chegando em alguns momentos a ficar abaixo da inflação ou até a dar prejuízo ao investidor.
Conclusão
Espero que este post tenha sido útil não só para mostrar o potencial de aplicação do pacote calcCidadao mas também para propor uma nova abordagem na análise de investimentos. De fato, retornos passados não indicam retornos futuros, ainda mais se tratando de indicadores financeiros. Contudo, uma simples análise probabilística pode ajudar a dirimir algumas incertezas na consideração de investimentos.