Lancei recentemente a versão 0.0.2 do pacote mafs tanto no CRAN como no Github. Adicionei dois novos recursos:
* No data frame df_models criado, foi acrescentada uma variável referente ao tempo de execução (runtime) do modelo para a série temporal de input. Isso foi uma necessidade devido ao fato de alguns modelos levarem muito tempo para rodar. Esse dado será importante para ser levado em consideração no segundo recurso adicionado:
* A função select_forecast() agora tem um argumento chamado dont_apply, no qual o usuário poderá inserir os modelos (em forma de vetor de caracteres) que não deverão ser usados na função para criar modelos preditivos. Esse recurso é muito útil para excluir da função os pacotes que demoram muito e que não costumam entregar bons resultados.
Neste post, farei uma demonstração da aplicação do pacote mafs em diversas séries temporais diferentes.
# carregar pacotes importantes
library(fpp)
library(dplyr)
library(ggplot2)
library(mafs)
library(magrittr)
library(ggrepel)Os dados
As séries temporais usadas pertencem ao pacote fpp, que disponibiliza as séries temporais usadas no livro do Hyndman.
Vamos armazenar essas diversas séries em uma lista:
data_fpp <- list(a10 = a10, ausair = ausair, ausbeer = ausbeer,
austa = austa, austourists = austourists,
cafe = cafe, debitcards = debitcards,
elecequip = elecequip, elecsales = elecsales,
euretail = euretail, guinearice = guinearice,
h02 = h02, livestock = livestock,
oil = oil, sunspotarea = sunspotarea,
usmelec = usmelec, wmurders = wmurders
)
# confirmando que todas as séries são objetos do tipo 'ts', que é a classe
# usada como input para a funcão select_forecast()
lapply(data_fpp, class) %>% unlist## a10 ausair ausbeer austa austourists cafe
## "ts" "ts" "ts" "ts" "ts" "ts"
## debitcards elecequip elecsales euretail guinearice h02
## "ts" "ts" "ts" "ts" "ts" "ts"
## livestock oil sunspotarea usmelec wmurders
## "ts" "ts" "ts" "ts" "ts"Será que todas essas séries são mensais? Podemos confirmar essa informação com a função frequency().
lapply(data_fpp, frequency) %>% unlist ## a10 ausair ausbeer austa austourists cafe
## 12 1 4 1 4 4
## debitcards elecequip elecsales euretail guinearice h02
## 12 12 1 4 1 12
## livestock oil sunspotarea usmelec wmurders
## 1 1 1 12 1# fazer um gráfico
lapply(data_fpp, frequency) %>% unlist %>% table %>% barplot()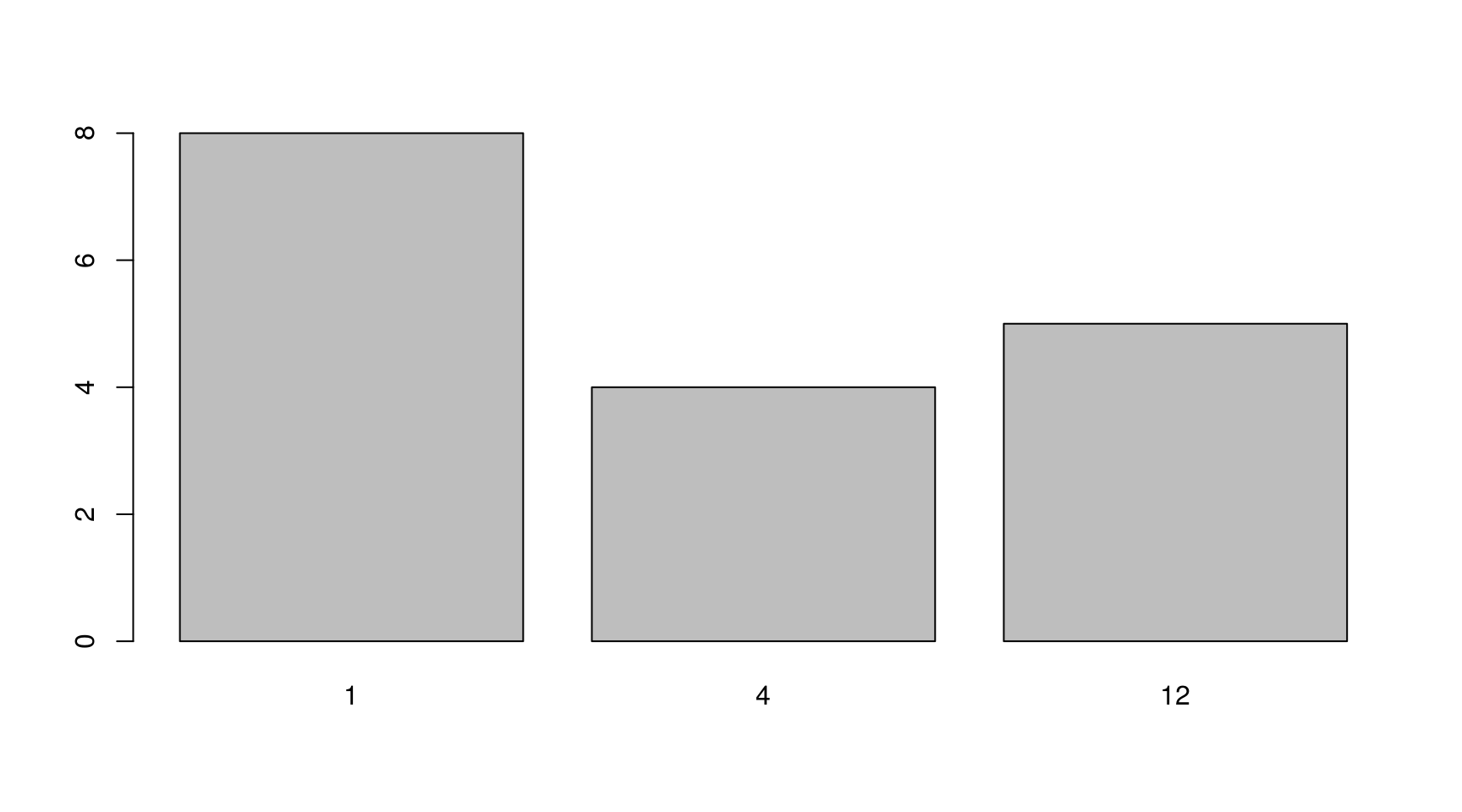
Temos então 8 séries anuais (frequência 1), 4 trimestrais e 5 mensais. Esse será um bom teste para o pacote mafs.
Modelagem
Para aplicar a função select_forecast() em todas as séries, é necessário um for loop:
# criar lista vazia para salvar os resultados
df_results <- vector("list", length = length(data_fpp))
# iniciar loop
for (i in 1:length(data_fpp)){
print(i)
# salvar serie do loop
data <- data_fpp[[i]]
# usar tamanho da serie de teste de 6. o horizonte de previsão não importa
# nao usar modelo híbrido apenas como demonstração do novo arg dont_apply
mafs_result <- select_forecast(data, test_size = 6, horizon = 3,
error = "MAPE", dont_apply = "hybrid")
mafs_result <- mafs_result$df_models
# acrescentar nome da série no dataframe dos resultados
mafs_result$serie <- names(data_fpp)[i]
df_results[[i]] <- mafs_result
}
# converter para data frame
df_results <- bind_rows(df_results)
saveRDS(df_results, "/home/sillas/R/data/2017-01-29-mafs02.Rds")Análise dos dados
Uma rápida visualização tabular dos resultados:
head(df_results)## model ME RMSE MAE MPE MAPE MASE
## 1 auto.arima -0.5266278 2.726579 2.317648 -3.404950 11.368897 1.867733
## 2 bats -0.6987866 2.543283 2.302901 -3.848498 11.063269 1.855849
## 3 croston 0.9954976 3.783578 2.770328 2.119148 11.608482 2.232536
## 4 ets -0.1664123 2.315405 2.059765 -1.141468 9.653898 1.659911
## 5 meanf 12.1695849 12.705245 12.169585 52.965233 52.965233 9.807155
## 6 naive -3.3000045 4.920821 4.586426 -17.426919 21.763365 3.696083
## ACF1 best_model runtime_model serie
## 1 -0.48291837 ets 1.508 a10
## 2 -0.50875972 ets 4.643 a10
## 3 -0.07557645 ets 1.717 a10
## 4 -0.49674756 ets 1.501 a10
## 5 -0.07557645 ets 0.001 a10
## 6 -0.07557645 ets 0.004 a10Vamos ver então quais modelos despontam como os mais rápidos e os mais eficientes.
Primeiro, um gráfico do tempo de execução por pacote
ggplot(df_results, aes(x = reorder(model, runtime_model, FUN = median),
y = runtime_model)) +
geom_boxplot() +
labs(x = NULL, y = "Tempo de execução (s)") +
coord_flip()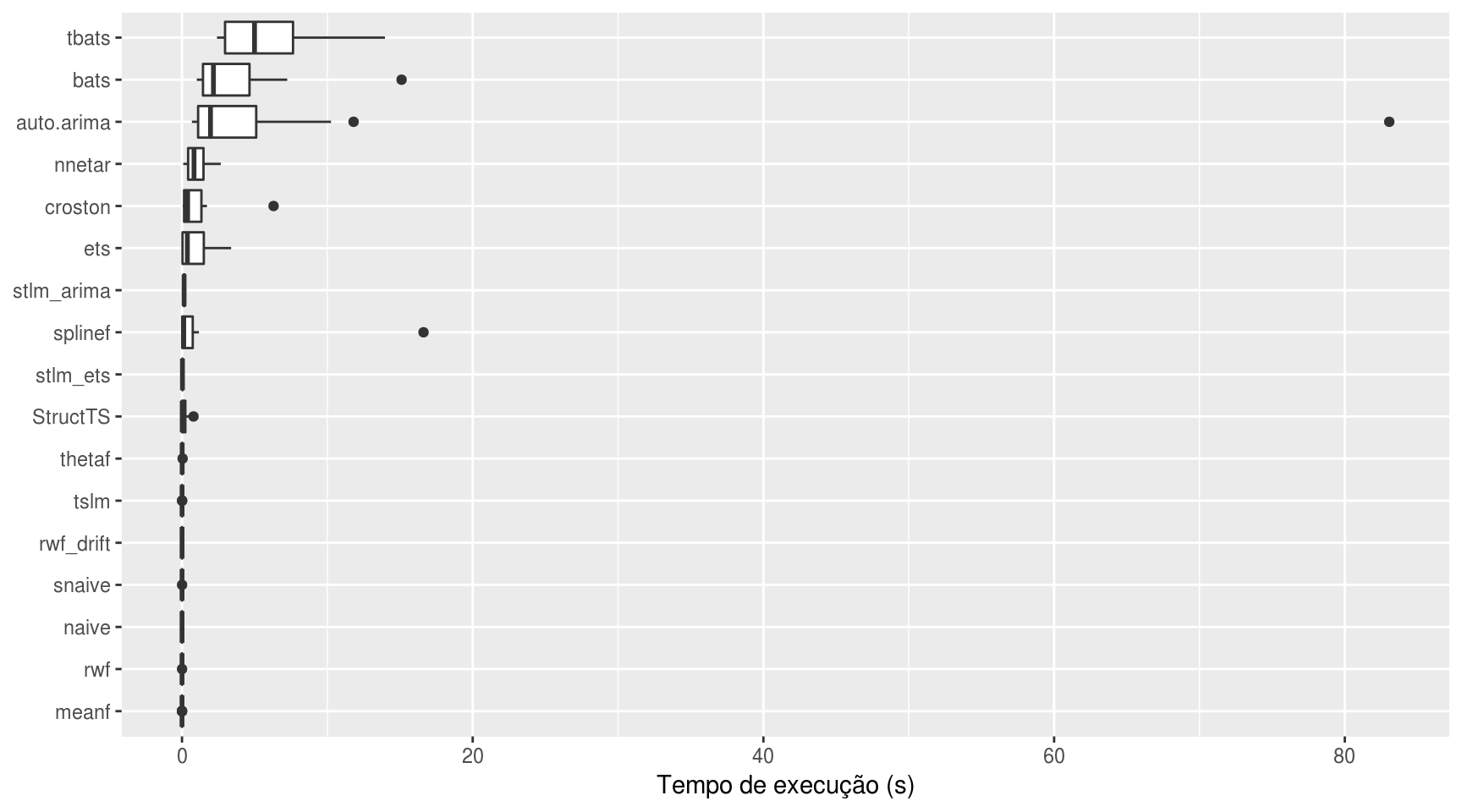
Percebe-se que os modelos tbats() e bats() são os mais computacionalmente custosos. Os mais rápidos são, sem surpresas, os modelos de previsão simples, como o da média simples e o modelo ingênuo.
Agora, um gráfico da acurácia dos modelos de acordo com a métrica MAPE:
ggplot(df_results, aes(x = reorder(model, -MAPE, FUN = median),
y = MAPE)) +
geom_boxplot() +
labs(x = NULL, y = "MAPE (%)") +
coord_flip()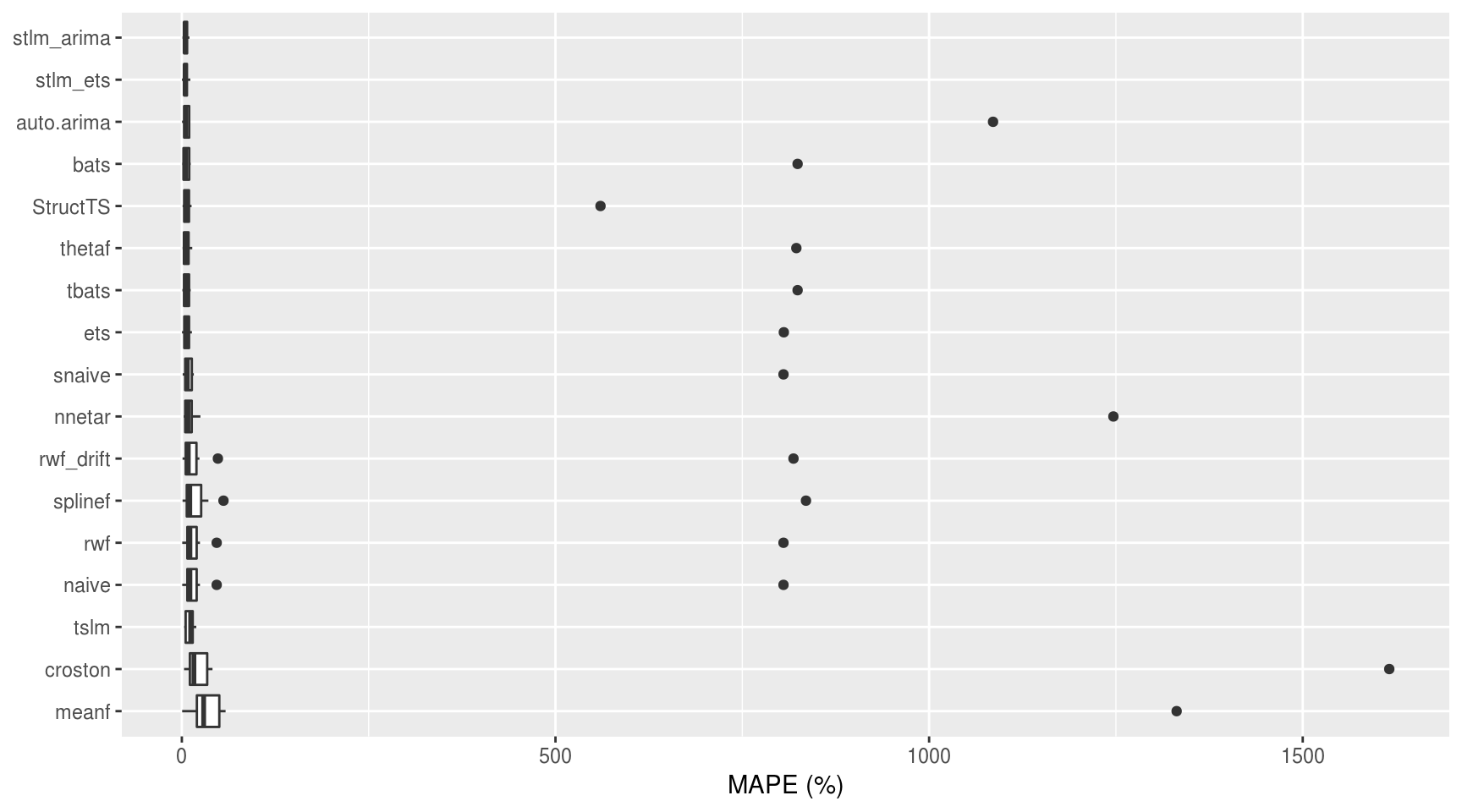
Alguns modelos apresentaram outliers, o que distorceu o boxplot. Visto que esse gráfico não serviu para muita coisa, é melhor resumir a acurácia por meio da mediana simples do MAPE:
# calcular a mediana do MAPE para cada modelo
df_results %>%
group_by(model) %>%
summarise(MAPE_mediano = median(MAPE)) %>%
ggplot(aes(x = reorder(model, -MAPE_mediano), y = MAPE_mediano)) +
geom_bar(stat = "identity") +
labs(x = NULL, y = "MAPE mediano") +
coord_flip() +
theme_bw()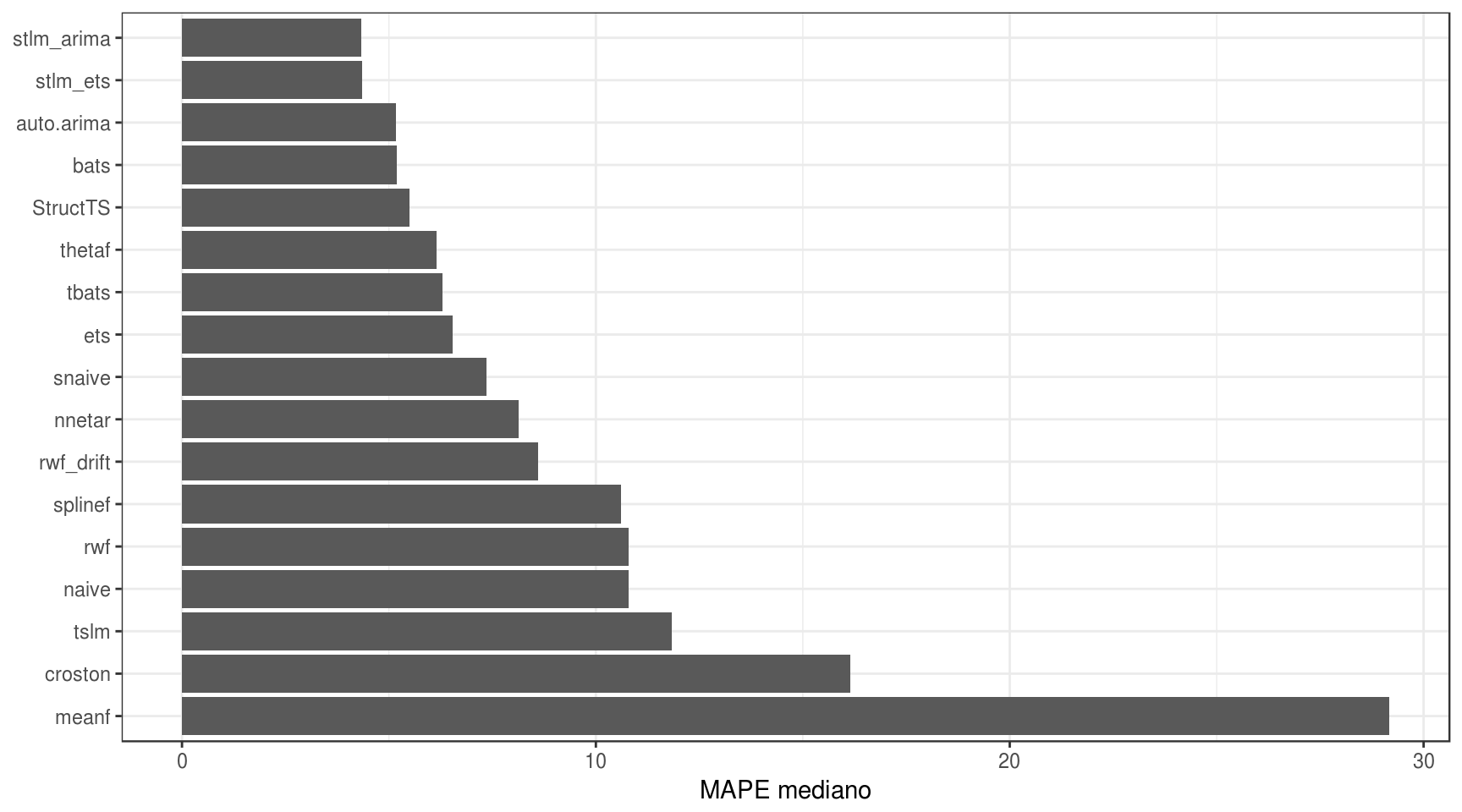
Vê-se que os modelos que obtiveram os melhores resultados foram os modelos stlm(), seja por arima ou por ets. Não vou entrar em detalhes estatísticos sobre o porquê desse resultado para não fugir do escopo do post.
Vamos então analisar a relação entre tempo de execução e eficácia dos modelos por meio de um gráfico de pontos.
ggplot(df_results, aes(x = runtime_model, y = MAPE)) +
geom_point() +
theme_bw()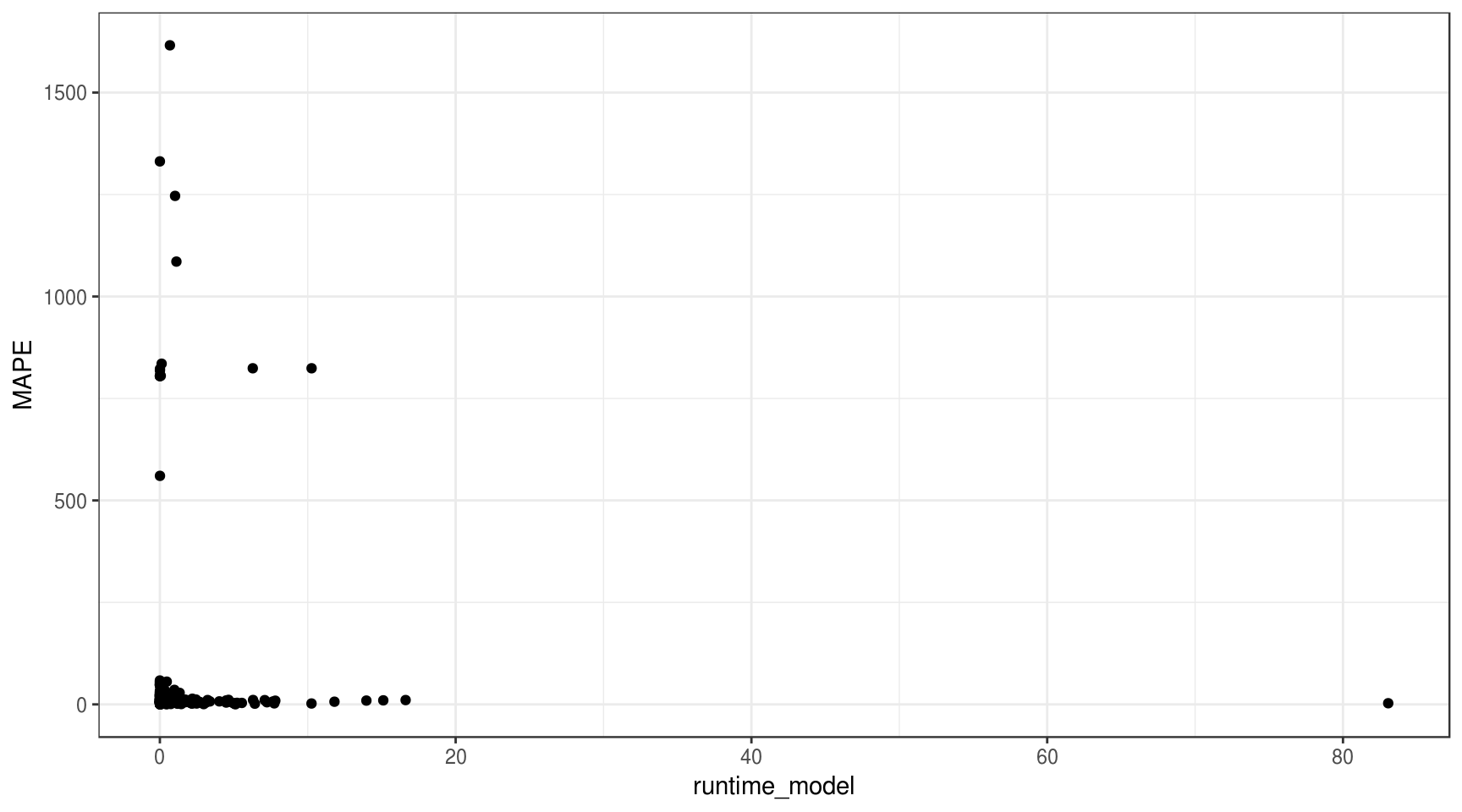
É difícil visualizar alguma relação muito clara nesse gráfico. Ao invés de plotar todos os data points, vamos resumir os dados pela mediana do MAPE e do runtime para cada modelo.
df_results %>%
group_by(model) %>%
summarise(MAPE_mediano = median(MAPE),
runtime_mediano = median(runtime_model)) %>%
ggplot(aes(y = runtime_mediano, x = MAPE_mediano)) +
geom_point() +
labs(y = "Tempo de execução mediano (s)",
x = "MAPE mediano (%)") +
geom_text_repel(aes(label = model)) +
theme_bw()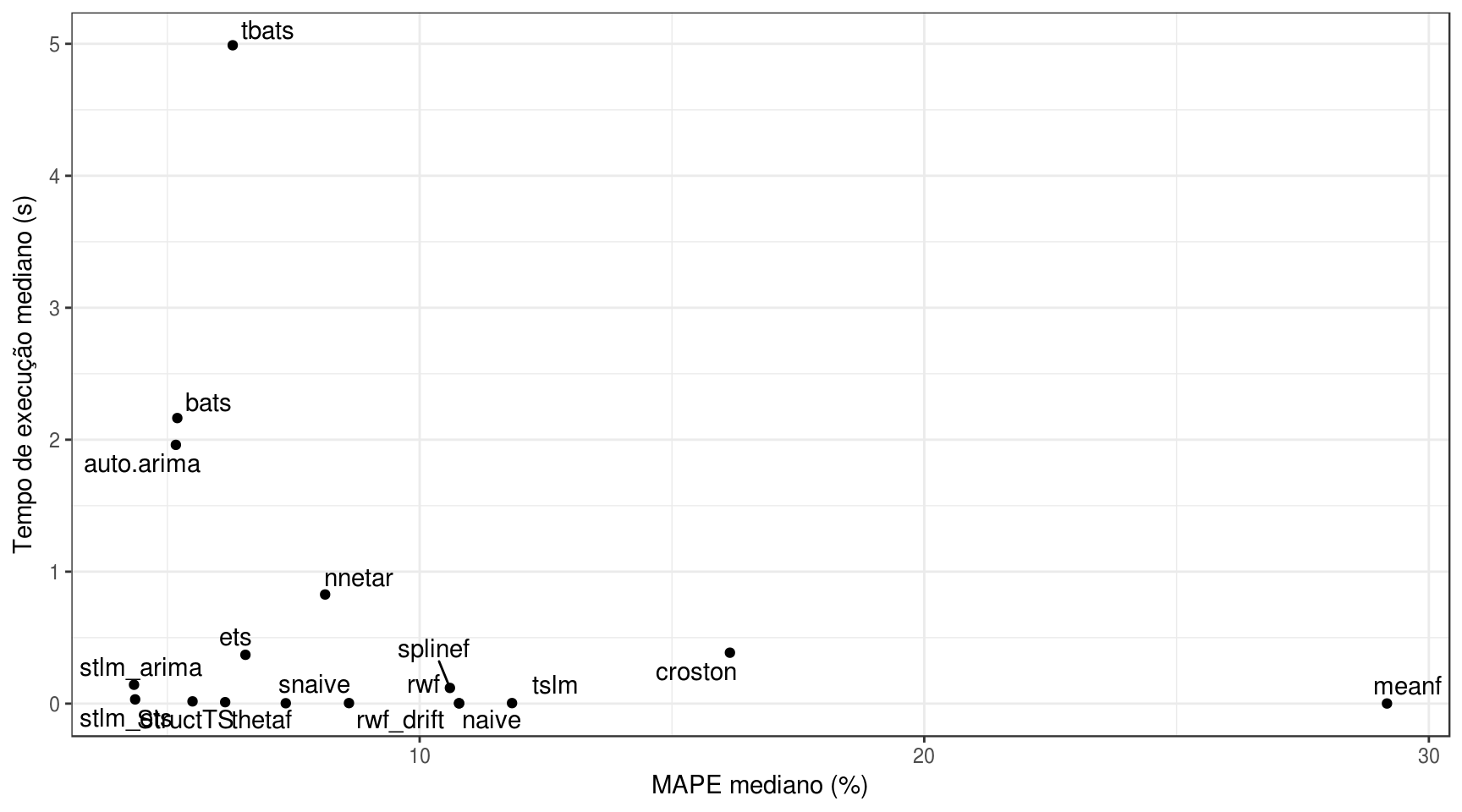
Novamente, não é possível determinar que a acurácia do modelo influencia o seu tempo de execução.
Análise da influência da frequência da série
Influência no tempo de execução
Já que estamos trabalhando ao mesmo tempo com séries trimestrais, mensais e anuais, por que não analisar a influência da variável da frequência da série nos resultados obtidos com o pacote?
Primeiro, vamos criar um data frame com características sobre as séries analisadas
df_series <- data.frame(
serie = names(data_fpp),
frequencia = lapply(data_fpp, frequency) %>% unlist,
tamanho_serie = lapply(data_fpp, length) %>% unlist
)
# juntar ao dataframe de resultados
df_results %<>% left_join(df_series, by = "serie")
names(data_fpp)## [1] "a10" "ausair" "ausbeer" "austa" "austourists"
## [6] "cafe" "debitcards" "elecequip" "elecsales" "euretail"
## [11] "guinearice" "h02" "livestock" "oil" "sunspotarea"
## [16] "usmelec" "wmurders"Para demosntrar a influência da frequência da série no tempo de execução dos modelos, uma boa opção de visualização é o gráfico de densidade:
df_results$frequencia %<>% as.factor
df_results %>%
filter(runtime_model <= quantile(runtime_model, 0.90)) %>%
ggplot(aes(x = runtime_model, color = frequencia)) + geom_density()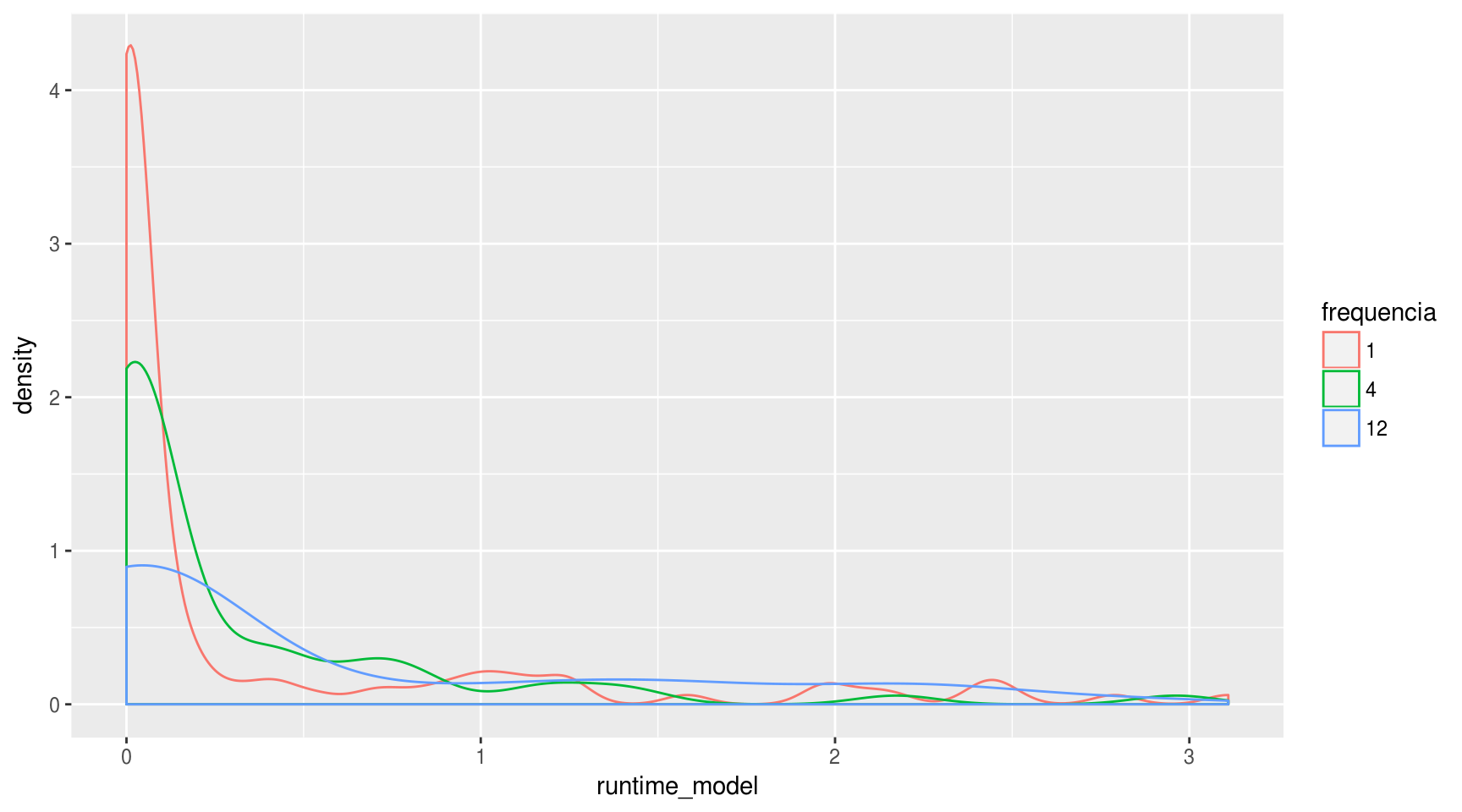
É difícil tirar qualquer tipo de conclusão a partir do gráfico acima. Dá para afirmar que a probabilidade de um modelo ter um runtime muito curto (de até 0,25 segundos) é menor para séries mensais e trimestrais do que para mensais.
Um teste estatístico que pode ser usado para mensura essa relação é o ANOVA e o teste de Tukey:
anova.fit <- aov(runtime_model ~ frequencia, data = df_results)
summary(anova.fit)## Df Sum Sq Mean Sq F value Pr(>F)
## frequencia 2 221 110.36 3.599 0.0287 *
## Residuals 262 8035 30.67
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# Teste de Tukey
anova.fit %>% TukeyHSD()## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = runtime_model ~ frequencia, data = df_results)
##
## $frequencia
## diff lwr upr p adj
## 4-1 0.4026234 -1.6041101 2.409357 0.8840947
## 12-1 2.0767411 0.1990179 3.954464 0.0260572
## 12-4 1.6741176 -0.4496095 3.797845 0.1530838O resultado do teste ANOVA aponta um valor significante (valor p menor que 0,05), o que indica que a hipótese nula de que a frequência da série não influencia o tempo de execução do ajuste pode ser rejeitado.
Já o teste de Tukey indica que apenas a hipótese nula só pode ser rejeitada para a comparação entre séries mensais e anuais. Para as outras duas comparações, o valor p é maior que 0,05.
Influência na acurácia
df_results %>%
filter(MAPE <= quantile(MAPE, 0.90)) %>%
ggplot(aes(x = MAPE, color = frequencia)) + geom_density()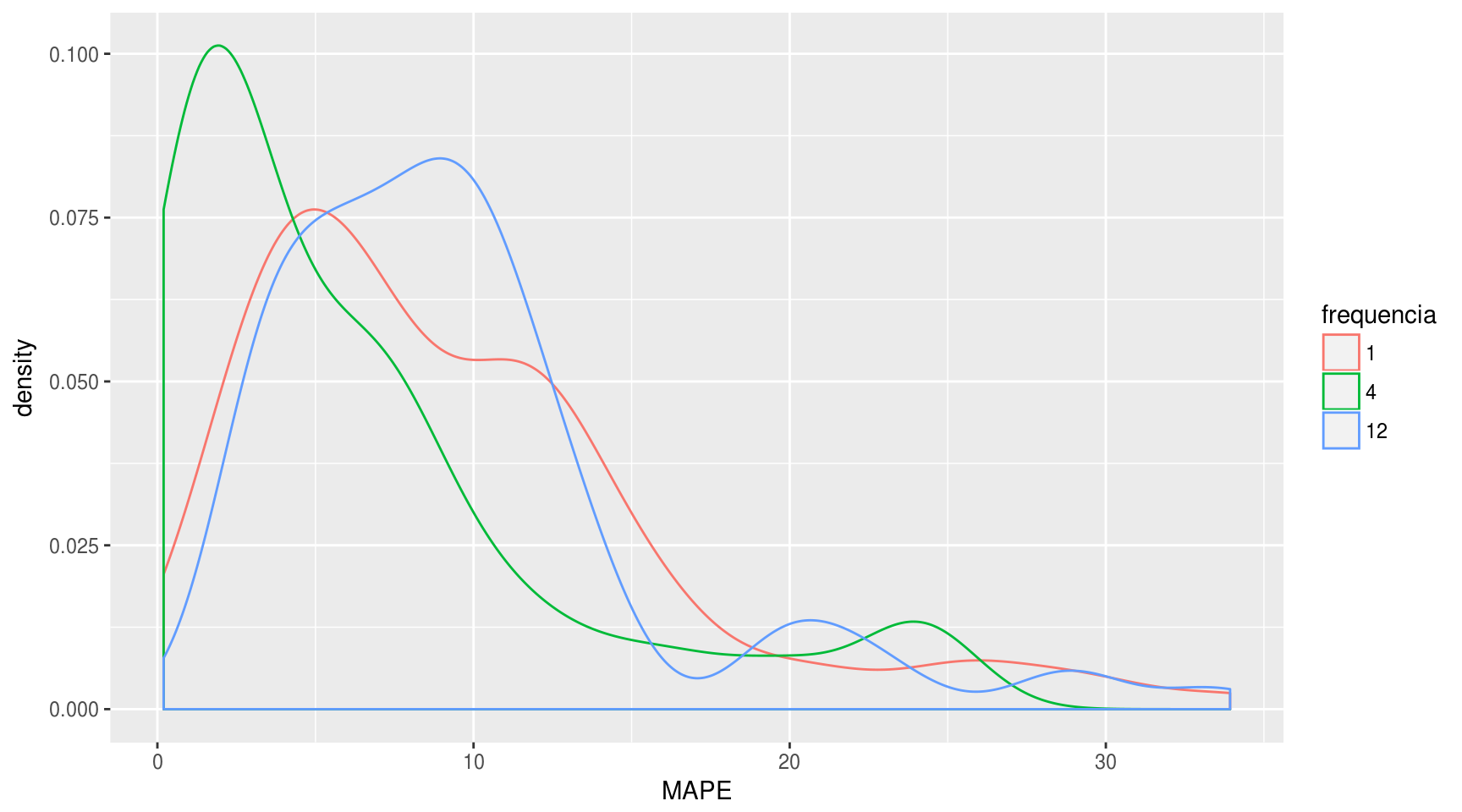
anova.fit <- aov(MAPE ~ frequencia, data = df_results)
summary(anova.fit)## Df Sum Sq Mean Sq F value Pr(>F)
## frequencia 2 900822 450411 10.14 5.71e-05 ***
## Residuals 262 11633340 44402
## ---
## Signif. codes: 0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1# Teste de Tukey
anova.fit %>% TukeyHSD()## Tukey multiple comparisons of means
## 95% family-wise confidence level
##
## Fit: aov(formula = MAPE ~ frequencia, data = df_results)
##
## $frequencia
## diff lwr upr p adj
## 4-1 -120.929333 -197.28734 -44.57133 0.0006774
## 12-1 -115.580724 -187.02977 -44.13168 0.0005011
## 12-4 5.348609 -75.46111 86.15832 0.9866718Conclusão
Uma próxima análise poderia incluir um número maior de séries e de frequências diferentes, como diárias e semanais.