Capítulo 4 Decomposição de Séries Temporais

# install.packages("seasonal")

library(BETS)
library(forecast)
library(lubridate)
library(tidyverse)
library(magrittr)
library(seasonal)

Séries Temporais podem exibir uma grande variedade de padrões que podem ser modelados separadamentes, o que pode ajudar o analista a entender melhor os dados e até mesmo a melhorar as previsões.

Já vimos no capítulo introdutório que uma série temporal possui três tipos de padrão: tendência, sazonalidade e ciclo. Se assumirmos que a série segue um modelo aditivo, então, matematicamente, ela pode ser descrita pela equação \(y_t = S_t + T_t + E_t\), onde \(E_t\) é o componente do erro no período \(t\). Se a série for melhor descrita por um modelo multiplicativo, então a equação vira \(y_t = S_t \times T_t \times E_t\).

Para se decidir se uma série segue um modelo aditivo ou multiplicativo (alguns algoritmos já calculam isso internamente), observe se a magnitude dos períodos sazonais ou a variância da tendência cresce conforme o nível (valores absolutos) da série cresce.

Por exemplo:

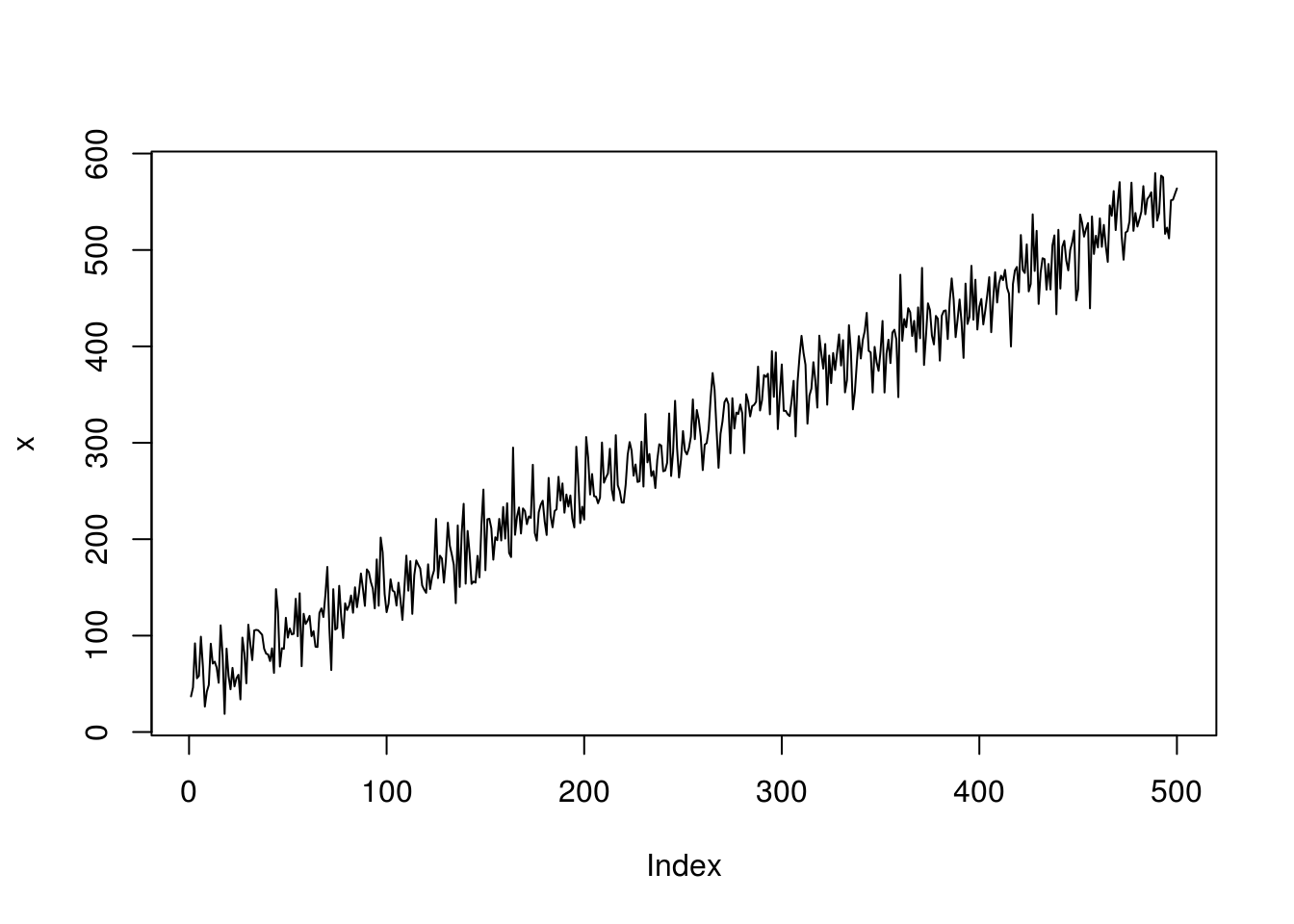
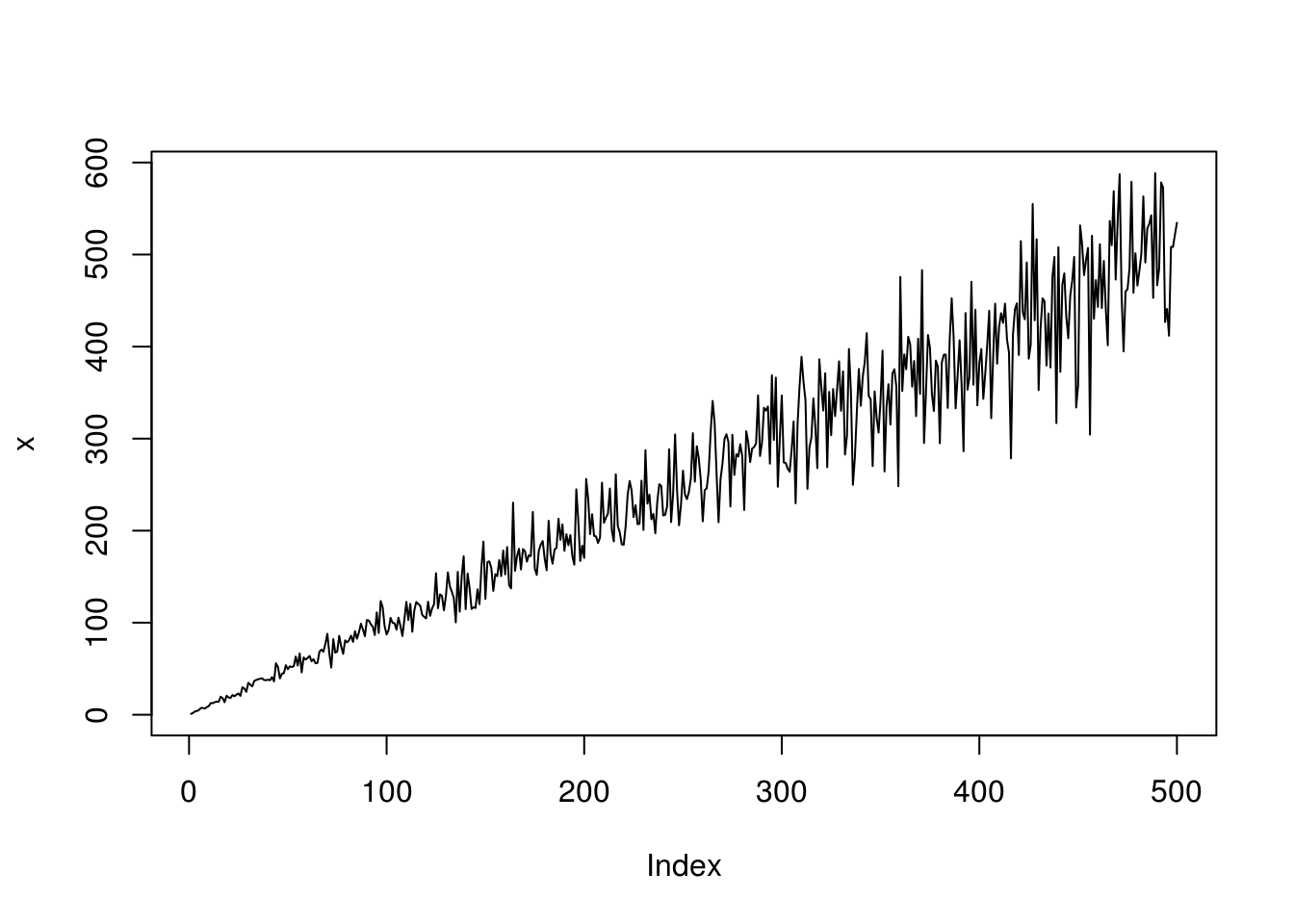
No segundo gráfico, vemos que, para valores maiores da série temporal, a variância dos dados é maior.

4.1 Médias móveis

Embora seja meio datada e tenha dado espaço para técnicas mais avançadas de decomposição, a média móvel é a base de muitos métodos de análises de séries temporais e uma importante etapa para estimar o componente de tendência de uma série.

Vamos voltar a analisar a série temporal baixada por meio do BETS:

energia <- readRDS("data/ts_energia.Rda")
# plotando a serie contra uma media movel de 3 meses
plot(energia)
ma(energia, 3) %>% lines(col = "red", lwd = 1)
# a media movel de 3 meses nao foi suficiente. vamos aumentar o periodo
ma(energia, 12) %>% lines(col = "blue", lwd = 2)
ma(energia, 24) %>% lines(col = "green", lwd = 3)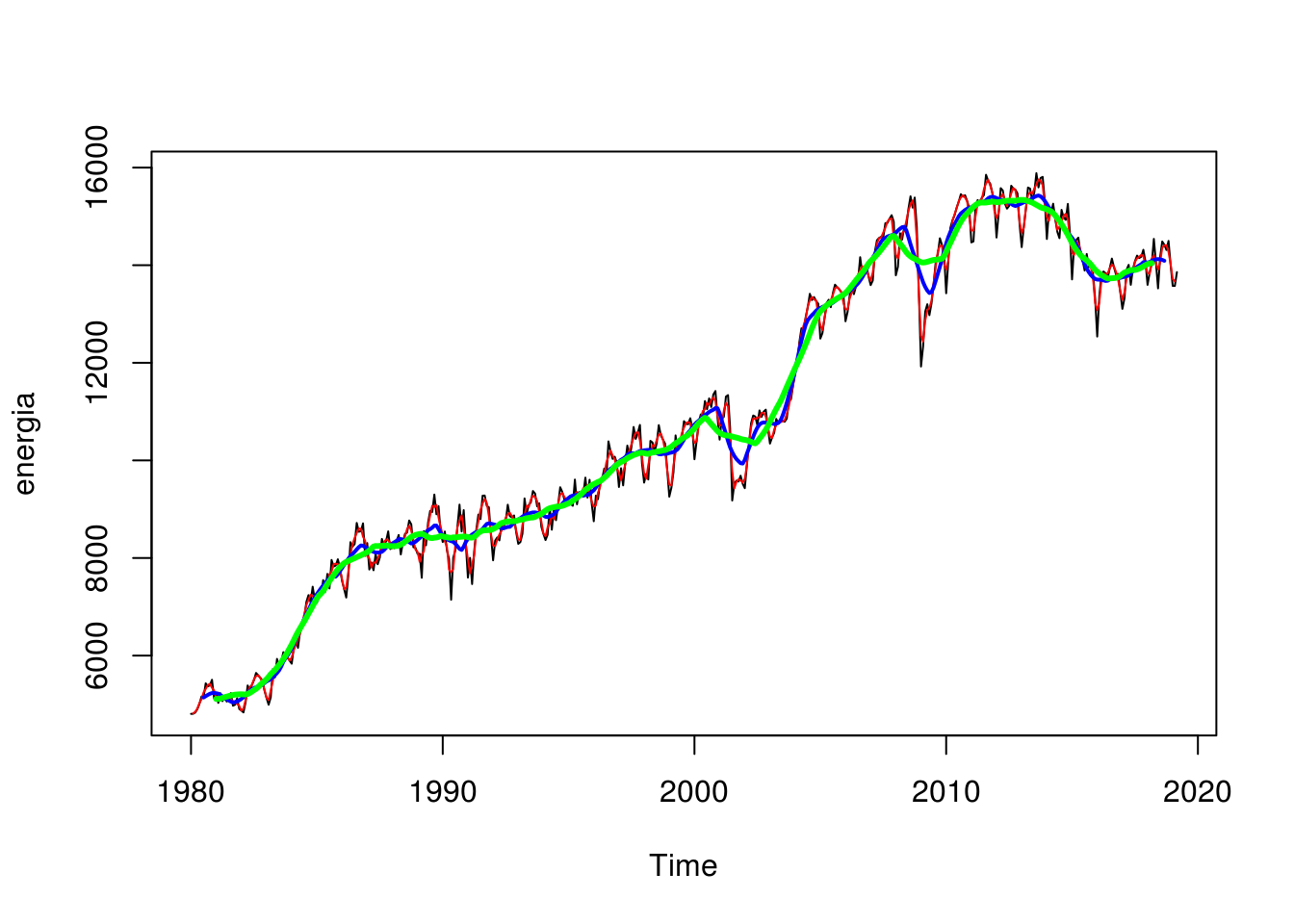

A curva que apresenta menos flutuações sazonais é verde, referente à média móvel de 24 períodos. Mesmo assim, pode-se dizer que essa decomposição não foi satisfatória, devido a curva apresentar perturbações mesmo usando um período longo (24 meses) para sua estimação.

4.2 Pacote `seasonal`

O pacote seasonal, disponível no CRAN, implementa uma interface ao algoritmo e software X-13-ARIMA-SEATS, desenvolvido pelo US Census Bureau. Possui recursos como seleção automática do modelo ARIMA, detecção de outliers e suporte para feriados definidos pelo usuário, como Carnaval e Páscoa.

Um rápido uso do pacote seasonal é mostrado abaixo:

m <- seas(energia)
# resumo sobre o modelo
summary(m)

## 
## Call:
## seas(x = energia)
## 
## Coefficients:
##                      Estimate  Std. Error z value             Pr(>|z|)    
## Leap Year            58.60609    56.18712   1.043             0.296924    
## Mon                 -25.25882    17.47502  -1.445             0.148339    
## Tue                 -18.16659    17.46348  -1.040             0.298218    
## Wed                 -54.46067    17.45878  -3.119             0.001812 ** 
## Thu                  92.24828    17.46016   5.283        0.00000012684 ***
## Fri                 -37.13352    17.62849  -2.106             0.035165 *  
## Sat                  11.39096    17.48081   0.652             0.514642    
## Easter[15]         -129.88101    37.31801  -3.480             0.000501 ***
## AO1990.May         -930.64663   163.15515  -5.704        0.00000001170 ***
## LS2001.Jul        -1706.97822   195.90208  -8.713 < 0.0000000000000002 ***
## LS2003.Dec          883.03805   196.12478   4.502        0.00000671810 ***
## AO2008.Dec         1004.92270   203.79179   4.931        0.00000081758 ***
## LS2008.Dec        -2099.78174   245.37722  -8.557 < 0.0000000000000002 ***
## MA-Nonseasonal-01     0.27018     0.04459   6.059        0.00000000137 ***
## MA-Seasonal-12        0.77013     0.03122  24.672 < 0.0000000000000002 ***
## ---
## Signif. codes:  0 '***' 0.001 '**' 0.01 '*' 0.05 '.' 0.1 ' ' 1
## 
## SEATS adj.  ARIMA: (0 1 1)(0 1 1)  Obs.: 471  Transform: none
## AICc:  6264, BIC:  6329  QS (no seasonality in final):1.115  
## Box-Ljung (no autocorr.): 34.74 . Shapiro (normality): 0.9928 *
## Messages generated by X-13:
## Notes:
## - Unable to test AO2008.Dec due to regression matrix
##   singularity.

# plotando o modelo
autoplot(m)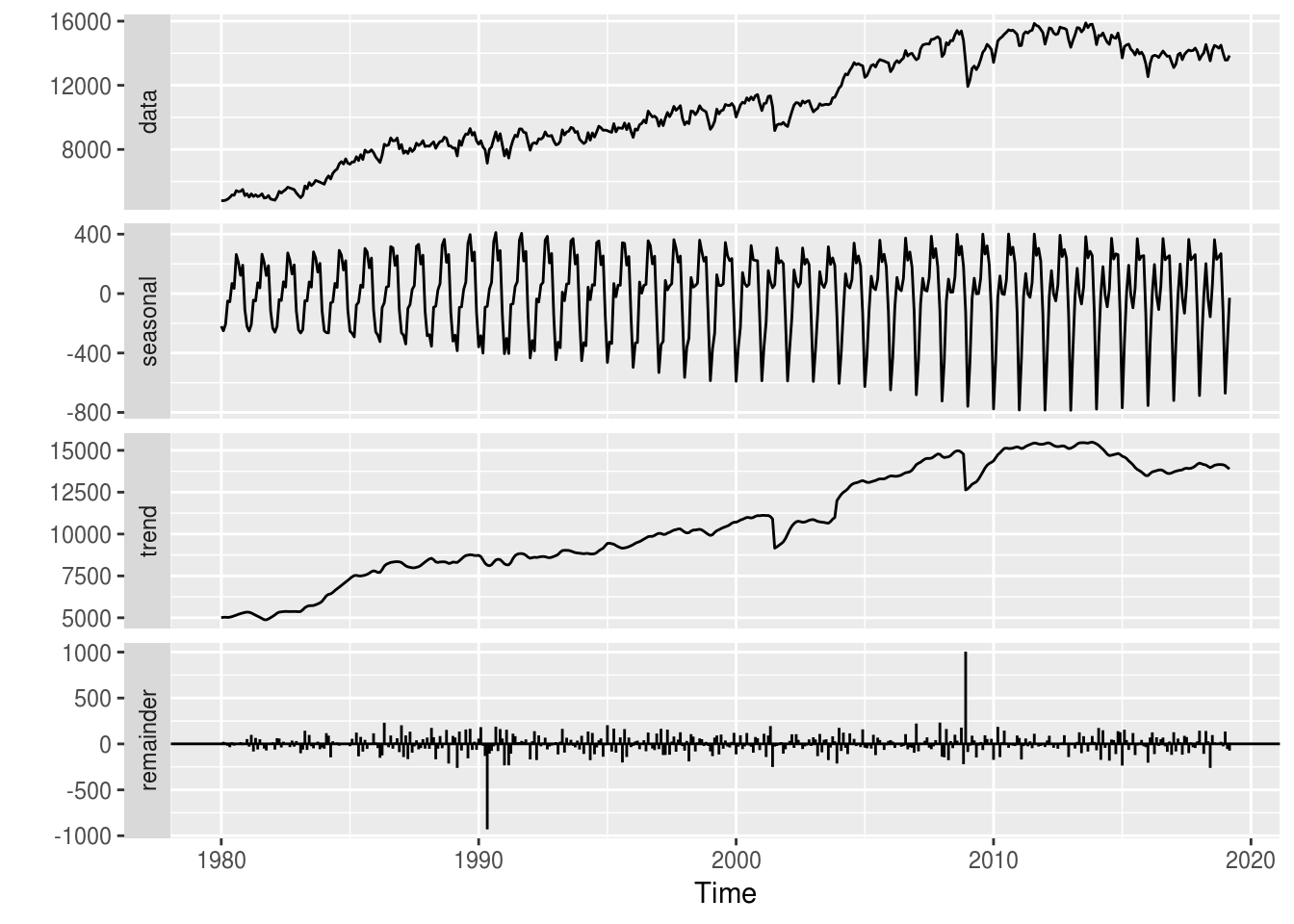

# retornando as componentes individuais da serie:

# seasonal(m)
# trendcycle(m)
# remainder(m)
# seasadj(m)

A função forecast::ggsubseriesplot() pode ser utilizada para avaliar como o componente sazonal variou com o passar do tempo:

m %>% 
  # extrair componente sazonal
  seasonal() %>% 
  # plotar grafico sazonal
  ggsubseriesplot()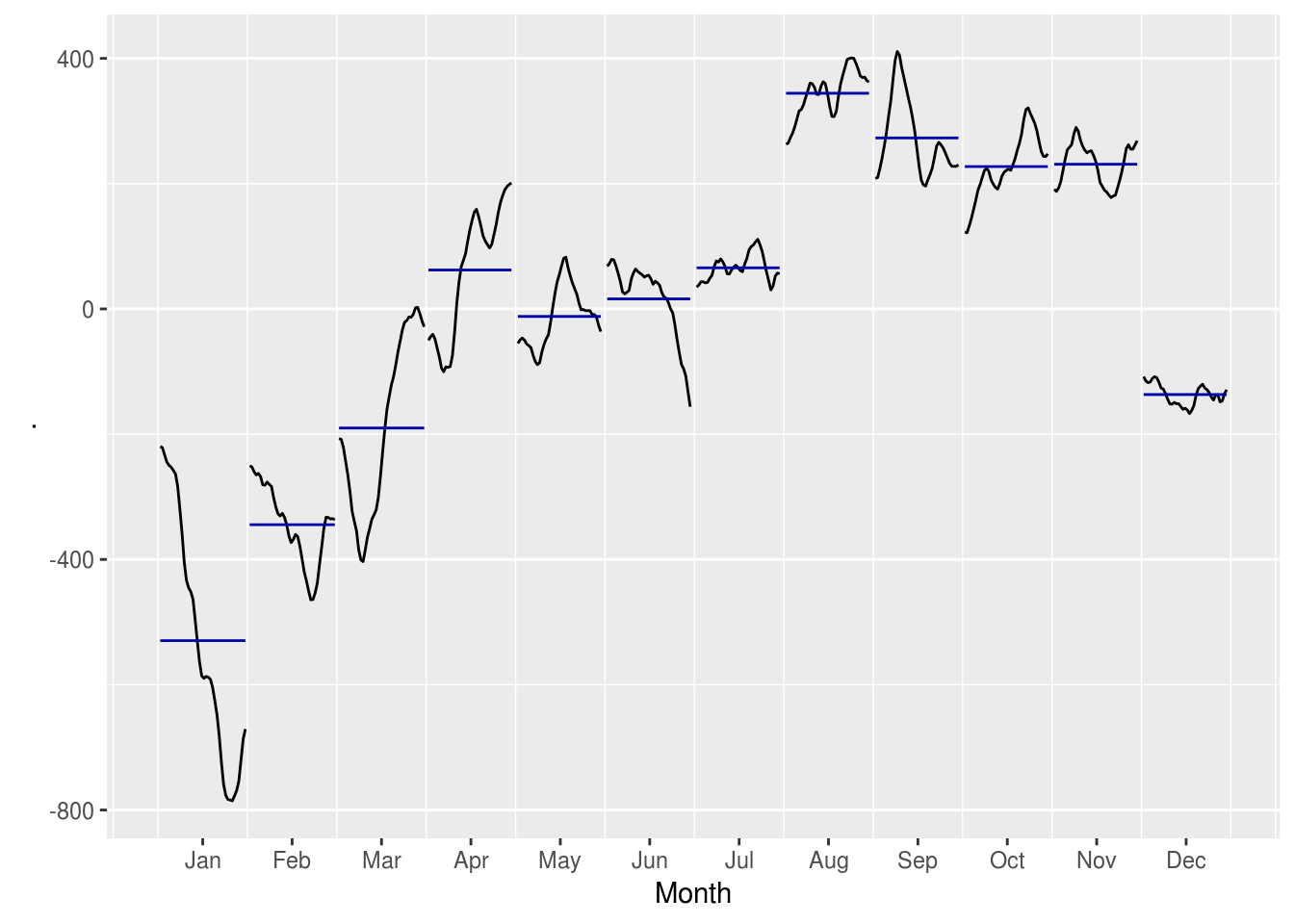

4.3 Mensurando a força dos componentes

https://otexts.com/fpp2/seasonal-strength.html

r_t <- remainder(m)
t_t <- trendcycle(m)
s_t <- seasonal(m)

measure <- function(R, c){
  x1 <- 0
  x2 <- 1 - var(R)/var(R + c)
  
  max(x1, x2)
}


measure(r_t, s_t)

## [1] 0.8596937

Capítulo 4 Decomposição de Séries Temporais

4.1 Médias móveis

4.2 Pacote seasonal

4.3 Mensurando a força dos componentes

4.2 Pacote `seasonal`